So everyone should understand the underlying concept of this principle. So read it carefully and keep patience. This principle is strictly based on the conservation of energy. However, we are talking about the topic of hydrodynamics.

Then which type of energy is involved in it. When Bernoulli was doing his research, he observed that, if any ideal fluid is non-viscous, incompressible, streamlined, and irrotational, then at every cross-section throughout the liquid flow, the sum of pressure energy, kinetic energy, and potential energy at per unit volume is constant. Then he expressed this mathematically as follows: $latexpage$
$$P+\frac{1}{2}\rho v^2+\rho gh=\text{constant}$$
Where P stands for pressure energy, $\frac{1}{2}\rho v^2$  stands for kinetic energy and $\rho gh$
Stands for potential energy.

Now we are going to see, that how did he come to this relationship, so the derivation is as follows:

DERIVATION BERNOULLI’S EQUATION

Let’s take $p_1$, $a_1$, $h_1$, $v_1$, and $p_2$, $a_2$, $h_2$, $v_2$, be the pressure, area of cross-section, height, and velocity of liquid flow at points A and B, respectively. Then the force acting on the fluid at point A is $F_1 = p_1a_1$
See the diagram below for a more precise understanding.

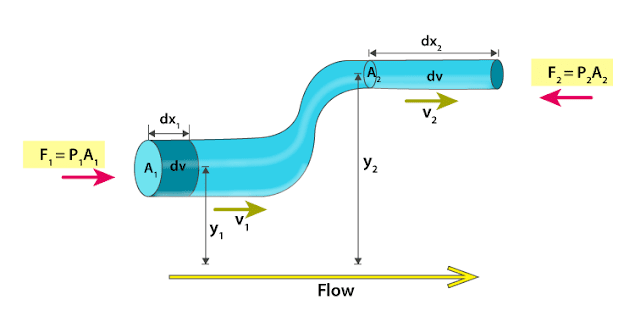
Then distance travel by the fluid in one second at point A is given as = v1×1=v1
Then work done per second on the fluid at point A is :
$$W1 = p_1a_1v_1$$
similarly, we can say that work done on second point B is, $$W_2 = p_2a_2v_2$$
Then network done by the pressure is given as pressure energy difference.
$$W=W_1-W_2=p_1a_1v_1-p_2a_2v_2$$
But from the equation of continuity, we know that ,
$$V = a_1v_1= a_2v_2 = \frac{m}{\rho}$$
So work done can be written as
$$W=\frac{p_1m}{\rho}-\frac{p_2m}{\rho}$$
This pressure energy of the fluid is further converted into kinetic energy and potential energy, because due to this pressure difference liquid flow from point A to another point B. From doing this liquid attain different heights i.e. From $h_1$ to $h_2$

It means this pressure energy is further balanced by the sum of the change of kinetic energy and potential energy.
$$\frac{p_1m}{\rho}-\frac{p_2m}{\rho}= \left(mgh_2 – mgh_1\right) +\left(\frac{mv_2^2}{2}-\frac{mv_2^2}{2}\right)$$
Cancelling m by taking common on both side we get-
$$\frac{\left(p_1 -p_2\right)}{\rho}=\left(gh_2-gh_1\right)+\left(\frac{v_2^2}{2}-\frac{v_1^2}{2}\right)$$
Multiplying ρ on RHS we get-
$$p_1-p_2 =\rho gh_2-\rho gh_1+\frac{\rho v_2^2}{2}-\frac{\rho v_1^2}{2}$$
Taking 1 marked on LHS and 2 marked on RHS , we get-
$$p_1+\rho gh_1+\frac{\rho v_1^2}{2}= p_2+\rho gh_2+\frac{\rho v_2^2}{2}$$
So both sides are Equal then we can conclude that-
$$p+\frac{1}{2}\rho v^2+\rho gh=\text{constant}$$
This mathematical modeling is done by Bernoulli in 1738.
But if both sides are divided by the $\rho g$, then we get-
$$\frac{p}{\rho g}+h+\frac{v^2}{2g}= \frac{\text{constant}}{\rho g}=\text{new constant}$$
Then, $\frac{p}{\rho g}$ is called pressure head and h is the gravitational head or potential head and
$\frac{v^2}{2g}$ is called velocity head.

This suggests that for an ideal fluid that is flowing in a pipe, then the sum of pressure head, gravitational head, and velocity head is always a constant.

Here a video is given to you for a better understanding.

FLUID IN HORIZONTAL PIPE

If the fluid is flowing in a horizontal pipe, then one element of the Bernoulli principle has been eliminated: its height, because the pipe is lying horizontally to the ground level so height is zero. Then for this type of conditions Bernoulli principle as follows:
$$p_1 + \frac{1}{2}\rho v_1^2 = p_2 +\frac{1}{2}\rho v_1^2$$
So it becomes
$$p+\frac{1}{2}\rho v^2=\text{constant}$$

FLUID AT REST

If fluid are in rest, then it’s velocity is zero, it means in Bernoulli equation, kinetic energy element is zero, in such conditions, this principle is as follows:
$$\begin{align*} p_1 + \rho gh_1& = p_2 + \rho gh_2\\ p_1- p_2 &= \rho g\left(h_2 – h_1\right) \end{align*}$$
Then, in constant form it is written as:
$$p + \rho gh =\text{constant}$$
This is all about the Bernoulli principle.