Cyclotron

We have seen in previous articles that hows a charged particle moves in the combined effect of an electric and magnetic field. Here, in this open article, we will discuss a well-known application of motion of charged particles in combined electric and magnetic fields i.e cyclotron. We will discuss the basics of cyclotron in detail, so let’s get started…

What is a cyclotron?

Cyclotron is a machine which is based on the principle of motion of charged particles in combined electric and magnetic field and used to accelerate the charged particles to a very high energies.

Cyclotron is invented by Ernest Orlando Lawrence in 1929–30 at the University of California, Berkeley. He invented this machine to study the nuclear structure of an atom with his colleague M.S Livingston. Further, he patented this invention in 1932. For his invention, he was awarded the 1939 Noble Prize in physics.

In a cyclotron charged particles are accelerated outwardly from the center of a flat cylindrical vacuum chamber along a spiral path. The particles are held to a spiral trajectory by a static magnetic field and accelerated by a rapidly changing (radio frequency) electric field

Working principle of cyclotron

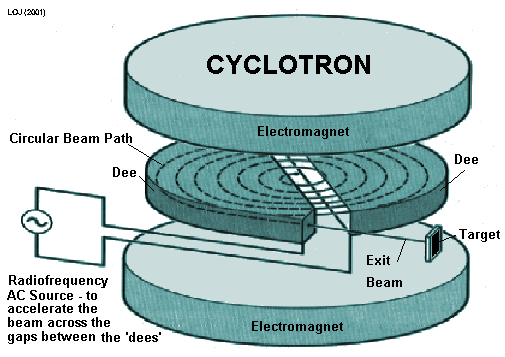
A cyclotron is a particle accelerator, which accelerates a beam of charged particles at very high speed with the help of a high-frequency alternating voltage which is applied between the two D shaped hollow metal plate electrodes, called “dees” in a vacuum chamber.

The dees were placed facing the narrow space between them, creating a cylindrical space within themselves through which particles could move. Particles are injected at the center of this space.

The dees are located between the poles of a large electromagnet imposing a static magnetic field B, perpendicular to the plane of the electrode. The magnetic field causes the orbits of the particles to bend into a circular shape due to the Lorentz force acting perpendicular to their direction of the motion.

If the speed of the particles is kept constant, then they will move in a circular path inside the dees under the influence of a magnetic field. However, an alternating radio frequency (RF) voltage of several thousand volts is applied between the dees.[latexpage]

Due to this high alternating voltage, a high alternating electric field is created in the space between the dees which accelerates the charged particles at a very high speed.

The frequency is set such that the particles complete one revolution during one voltage cycle. For this, the frequency of the alternating voltage must equal the particle’s cyclotron resonance frequency.
$$f=\frac{qB}{2\pi m}$$ where B is the magnetic field strength, q is the charged particle, m is the relativistic mass of the charged particle.

What happens to the charged particle in the cyclotron?

Suppose a proton is injected at the center of the gap between the dees electrodes. Initially, it will move towards the negatively charged dee because positively charged particle experiences an electric force in the same direction as of electric field (direction of an electric field is always from positive to negative terminal).

Due to the electric force, the proton accelerates and enters into the negatively charged dee. Once it entered into the dee, then it is shielded from the electric field by the walls of the dees (electrostatic shielding), i.e electric field does not enter into the dee. It always perpendicularly emanates out from the surface of the dees. But it is not shielded from the magnetic field. It entered into the plane of the dees perpendicularly and in the effect of magnetic field proton continues to moves in a circular motion.

When the charged particles pass from dee electrode to the other then the polarity of the RF voltage reverses. Due to this, each time whenever the charged particles cross from one dee to another, the electric field is in the correct direction accelerates the proton into the negatively charged dee.

In fact, in cyclotron charged always keep chasing the oppositively charged dee. If we are using any negatively charged particle, then it will always chase the positively charged dee. It is because if the particle is negatively charged then the direction of electric force is always opposite to the direction of electric field.

Due to this acceleration, charged particle each time (during entering one dee to another) experiences a little push, and hence, the speed of the particle increases causes them to move in a circle of the larger radius with each revolution, so the particles move in a spiral path outward from the center to the rim of the dees. The radius of the spiral orbit of the charged particle which is dependent of the velocity can be given as- $$r=\frac{mv}{qB}$$

When the charged particle reaches near the rim of the dee electrode, a small voltage on a metal plate deflects the beam of the particle so it exits the dees through a small gap between them, and it hits a target located at the exit point at the rim of the chamber or leaves the cyclotron through an evacuated beam tube to hit the remote target.

Energy of charged particle in the cyclotron

Since the particles in a cyclotron are accelerated many times over by the voltage, the final energy of the particles does not depend on the accelerating voltage, but on the strength of the magnetic field and the diameter of the accelerating chamber, the “dees”. They only accelerate particles to the speeds that are much slower than the speed of light, not relativistic speeds. For non-relativistic particles the centripetal force $\displaystyle {F _ {\mathrm {C}} \;}$, which is necessary to keep them on their curved path, is given as:

$${\displaystyle F _ {\rm {C }} = {mv ^ {2} \over r} \;}$$

where ${\displaystyle m \;}$ is the mass of the particle, ${\displaystyle v \;}$ is its speed and ${\displaystyle r \,}$ the radius of the circular orbit. This force is provided by the Lorentz force ${\displaystyle F (B) \,}$ of the magnetic field ${\displaystyle B \,}$

$${\displaystyle F (B) = qvB \;}$$

Where ${\displaystyle q \,}$ is the strength of the charged particle. The particles attend their maximum energy when they reach the periphery of the Dees, where the radius of their orbit ${\displaystyle r \; = \; R}$ the radius of the dees. By equating these two forces, we get

$${\displaystyle {mv ^ {2} \over R} = qvB \;}$$

$${\displaystyle v = {qBR \over m} \,}$$

So the output energy of the charged particle in the form of kinetic energy is expressed as-

$$\boxed {{\displaystyle E = {1 \over 2} mv ^ {2} = {\frac {q ^ {2} B ^ {2} R ^ {2}} {2m}} \;} }$$

Uses and advantages of the cyclotron

Some uses and advantages of the cyclotron are given below:

• Cyclotrons were the best source of high-energy rays for nuclear physics experiments for several decades.
• Several cyclotrons are used for the research purpose, the results of which make it possible to calculate various properties, such as the average distance between atoms and the formation of various collision products.
• Cyclotrons can be used in particle therapy to treat cancer.
• Cyclotron rays, like proton therapy, can be used to penetrate the body and kill tumors from radiation damage while minimizing the damage to healthy tissue on their way.
• Cyclotron beams can be used to bombard other atoms to create short-lived positron-emitting isotopes suitable for PET imaging.
• More recently, some cyclotrons currently installed in hospitals for the production of radioisotopes have been upgraded to produce 99 million technetium. Technetium-99m is a diagnostic isotope that is in short supply due to difficulties at the Chalk River, Canada facility.

Limitations of the cyclotron

Some limitations of the cyclotron are given below:

• The energy to which the particles can be accelerated in a cyclotron is limited due to the change in mass with the speed.
• Neutral particles cannot be accelerated by a cyclotron.
• Only charged particles like protons, neutrons, and alpha particles can be accelerated by the cyclotron and the electron cannot accelerate. Because the mass of the electron is very small and a small increase in the energy of the electron causes it to move at a very high speed, thereby quickly deflecting the electrons from the oscillating electric field.

Watch this video for more visual understanding of the cyclotron.

Stay tuned with Laws Of Nature for more useful and interesting content.