So today we are going to talk about a very important and interesting concept of hydrodynamics i.e. equation of continuity. So, let’s get started…
Continuity means anything which covers equal displacement in an equal time interval.
In fluid mechanics, if V volume of liquid is entering in $\Delta t$ then the same volume of liquid is exiting in $\Delta t$ also. Fluid has so many properties, but the property by which it became unique, is the property of incompressible, which means fluid can’t be compressed by any means, Here fluid means liquid.
In hydrodynamics, we consider an ideal fluid, because the mathematical modeling of real fluid is very complicated.
An ideal fluid is a fluid that is non-viscous, incompressible, and irrotational.
So it is observed that when an ideal fluid flows through the pipe of different cross-sectional areas, the volume of fluid that is entering is equal to the volume of fluid which is an exit.
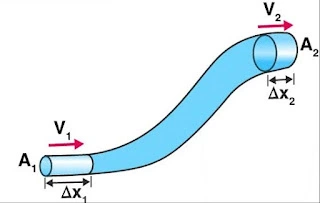
If the fluid is ideal then its density is constant at every point. If the volume is equal and its density is constant then the mass of fluid that is entering is also equal to the mass of fluid that is coming out. $$ V = \frac{m_1}{\rho} = \frac{m_2}{\rho}\qquad \text{then} \qquad m_1 = m_2$$ Conservation of mass is applying here.
What is the equation of continuity?
The equation of continuity is a fundamental equation in fluid mechanics that describes the conservation of mass in a fluid system. It states that the rate at which fluid is flowing into a given pipe must equal the rate at which it is flowing out of that pipe. Mathematically, the equation is expressed as:
$$A_1v_1 = A_2v_2 = \text{constant}$$
where $v_1$ is the velocity of the fluid when it is flowing in, $A_1$ is the cross-sectional area of the pipe at the initial end, and $v_2$ is the velocity of the fluid when it is flowing out, and $A_2$ is the cross-section of the pipe at final end. The equation is based on the principle of conservation of mass and is used to analyze the behavior of fluids in various flow systems, such as pipes, channels, and tanks.
Derivation of the continuity equation, class 11
Let’s take a pipe of the different cross-sectional areas with one end having $A_2$, $v_2$, $\Delta t$,$P_2$,$\rho_2$ and at the second end $A_1$, $v_1$, $\Delta t$, and $P_1$, $\rho_1$. Here $\Delta t$ is a small-time interval in which fluid gets displaced. And $\rho_1 =\rho_2$ due to the ideal nature of the fluid.
We know that the mass of fluid that is entering is equal to the mass of fluid that is coming out, so $m_2 = m_1$
And $m_2=V\rho_2$ , and $m_1 = V\rho_1$. Then we can say that $V\rho_2=V\rho_1$
Then, the Volume is given as-
$$
V =\text{cross sectional area}\times \text{displacement}
$$
So, $V=A_2v_2\Delta t$ and $V=A_1v_1\Delta t$
Putting value we get-
$$
A_2v_2\Delta t\rho_2=A_1v_1\Delta t\rho_1$$
But $\rho_2=\rho_1$ So, we get after canceling $\Delta t$ and $\rho$ both sides
$$
V = A_1v_1 = A_2v_2 = \text{constant}
$$ This is the equation for the equation of continuity.
Derivation of equation of continuity in differential form
The equation of continuity can be derived from the principle of conservation of mass. According to this principle, the total mass of a fluid in a system remains constant unless added to or removed from the system.
Consider a control volume within a fluid, which can be thought of as a three-dimensional region surrounded by a closed surface. The mass of fluid within the control volume can change due to two sources: fluid flowing into the control volume and fluid flowing out of the control volume.
Let the rate of fluid flowing into the control volume be represented by $𝑁_{\text{in}}$ and the rate of fluid flowing out of the control volume be represented by $𝑁_{\text{out}}$. Then, the rate of change of mass within the control volume is given by:
$$\frac{\Delta m}{\Delta t} = 𝑁_{\text{in}} – 𝑁_{\text{out}}$$
where $\displaystyle \frac{\Delta m}{\Delta t}$ is the rate of change of mass within the control volume and $\Delta t$ is the time interval.
Now, consider the volume flow rate, which is the volume of fluid that flows through a given cross-sectional area per unit of time. Let the cross-sectional area of the control volume be represented by $A$ and the velocity of the fluid be represented by $V$. Then, the volume flow rate can be expressed as:
$$Q = V A$$
where $Q$ is the volume flow rate. Combining the above equations, we can write:
$$\frac{\Delta m}{\Delta t} = 𝑁_{\text{in}} – 𝑁_{\text{out}} = \frac{(Q_{\text{in}} – Q_{\text{out}})}{ \rho}$$
where $Q_{\text{in}}$ and $Q_{\text{out}}$ are the volume flow rates of fluid flowing into and out of the control volume, respectively, and $\rho$ is the density of the fluid.
Using the divergence theorem, we can rewrite the above equation as:
$$\frac{\Delta V}{\Delta t} + \nabla . (VA) = 0$$
where $\nabla . (VA)$ is the rate of fluid flowing across any given surface, and the equation represents the equation of continuity.
This equation states that the rate of fluid flowing into the control volume must equal the rate of fluid flowing out of the control volume, which is based on the principle of conservation of mass.
Applications of the equation of continuity
The equation of continuity has many applications in various fields of physics and engineering, including:
- Fluid mechanics: The equation of continuity is widely used in the analysis of fluid flow in pipes, channels, tanks, and other flow systems. It helps to determine the velocity and pressure distributions in the fluid, which are important in the design of fluid transport systems.
- Aerospace engineering: The equation of continuity is used in the design and analysis of aerodynamic systems, such as wings and engines, to determine the flow of air over the surfaces and its effects on lift, drag, and propulsion.
- Heat transfer: In heat transfer applications, the equation of continuity is used to determine the flow rate of heat-carrying fluids, such as air or water, in heating and cooling systems.
- Chemical engineering: The equation of continuity is used in the design of chemical reactors to determine the flow rate of reactants and products, which is important in optimizing the reaction kinetics and efficiency.
- Electrical engineering: In electrical engineering, the equation of continuity is used to analyze the flow of current in electrical circuits, which is important in the design of power systems and electrical networks.
- Geophysics: The equation of continuity is used in geophysics to analyze the flow of fluids in the subsurface, such as groundwater or petroleum.
These are just a few of the many applications of the equation of continuity. The equation is a fundamental concept in fluid mechanics and is widely used to analyze fluid flow in a variety of systems.
Importance of the continuity equation
The continuity equation is important for several reasons:
- Mass Conservation: The continuity equation is based on the principle of mass conservation, which states that the total mass of a fluid in a system remains constant unless added to or removed from the system. The continuity equation helps to ensure that the rate at which fluid is flowing into a given region equals the rate at which it is flowing out of that region.
- Analysis of Fluid Flow: The continuity equation is a fundamental equation in fluid mechanics and is used to analyze the flow of fluids in pipes, channels, tanks, and other flow systems. It helps to determine the velocity and pressure distributions in the fluid, which are important in the design of fluid transport systems.
- Efficient and Reliable Operation: By ensuring the continuity of fluid flow, the continuity equation helps to ensure the efficient and reliable operation of fluid transport systems, such as pipes and channels.
- Understanding of Physical Systems: The continuity equation provides insight into the behavior of physical systems, such as fluid flow, and helps to identify conditions that can lead to instability or other issues.
- Interdisciplinary Applications: The continuity equation has many interdisciplinary applications, including aerospace engineering, heat transfer, chemical engineering, electrical engineering, and geophysics, among others.
The continuity equation is a fundamental concept in fluid mechanics and has many important applications in a variety of fields. It helps to ensure the continuity of fluid flow and provides valuable insight into the behavior of physical systems.
Watch this video for more reference.
Frequently Asked Questions – FAQs
What is the principle of continuity?
The principle of continuity is a concept in fluid mechanics that states that the flow of a fluid must be continuous and smooth, without any abrupt changes in velocity or direction. In other words, the fluid must move without interruption, and the velocity and direction of flow must vary smoothly and continuously throughout the fluid.
The principle of continuity is based on the concept of mass conservation, which states that the total mass of a fluid in a system remains constant unless added to or removed from the system. In a fluid system, this means that the rate at which fluid is flowing into a given region must equal the rate at which it is flowing out of that region.
This principle has important implications in the analysis of fluid flow, particularly in the design of fluid transport systems, such as pipes, channels, and tanks. It helps to ensure that the flow of fluid is smooth and continuous, which is essential for efficient and reliable operation of these systems.
The principle of continuity is often expressed mathematically using the equation of continuity, which is a fundamental equation in fluid mechanics that relates the rate of fluid flowing into and out of a given region to its velocity and cross-sectional area.
Where is the Equation of Continuity used?
The continuity equation is a very useful tool for determining the flow of fluids and their behaviour in a pipe or hose. The Continuity Equation is used on tubes, pipes, rivers, ducts with flowing fluids or gases, and many other structures.
What is the importance of the continuity equation?
In fluid dynamics, the continuity equation proves the law of mass conservation.
Why equation of continuity is called so?
This is a statement of the mass conservation principle for a one-dimensional steady flow with one inlet and one outlet. This is referred to as the continuity equation for steady one-dimensional flow.
Define continuity equation.
The product of the cross-sectional area of the pipe and the velocity of the fluid at any given point along the pipe is constant, according to the continuity equation.
Stay tuned with Laws Of Nature for more useful and interesting content.


