In this article, we will derive an Expression for energy and average power stored in an inductor, so let’s get started…
What is an inductor?
Inductor Definition: An inductor, also known as a coil, choke, or reactor, is a two-terminal passive electrical component that stores energy in a magnetic field when an electric current is passed through it. An inductor usually consists of an insulated wire wound into a coil.
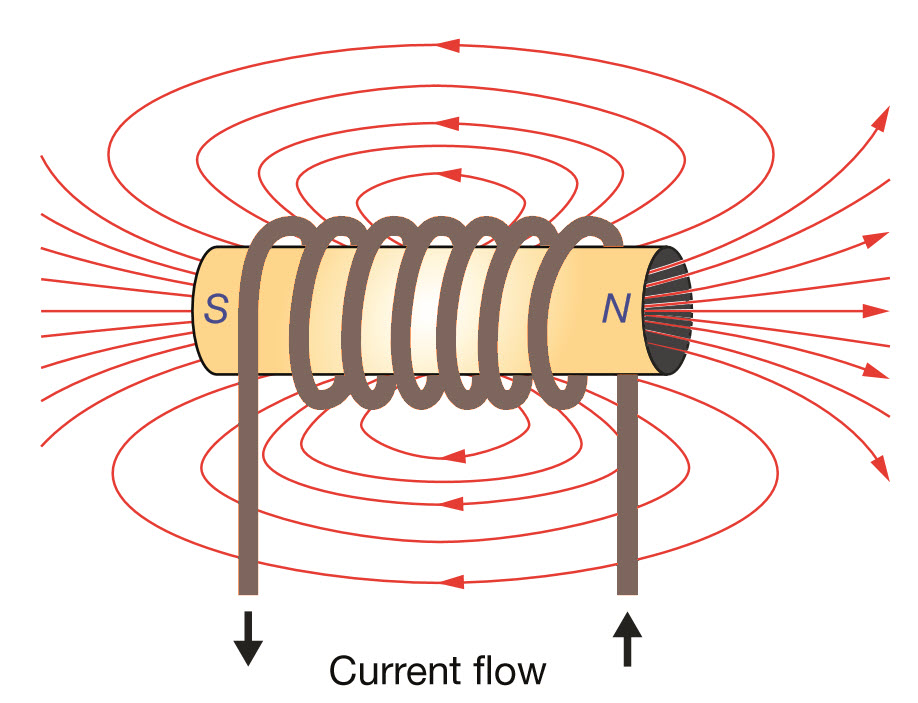
As the current flowing through the coil changes, the time-varying magnetic field induces an electromotive force (emf) (voltage) in the conductor that is described by Faraday’s law of induction. According to Lenz’s law, the induced voltage has a direction such that it opposes the change in current that created it. As a result, the inductors counteract any change in current through them.
Read Also
- Inductance – definition, formula, units, and dimensions
- Self-inductance | definition, formula, units, and dimensions
- Self-inductance of a long solenoid class 12
Expression for Energy stored in an inductor
Energy stored in an inductor: When an inductor is connected to a source of emf, the current starts growing through it. An induced emf is set up in the inductor which opposes the growth of current through it. The external source has to expend energy in building up the current through the inductor against the induced emf. This energy is stored in the inductor as magnetic field energy.
Let $I$ be the current through the inductor $L$ at any instant $t$. The current rises at the rate of $d I / d t$. So the induced emf is
$$
\mathcal{E}=-L \frac{d I}{d t}
$$
The work done against the induced emf in small time $d t$ is
\begin{aligned}
dW&=Pdt=-\mathcal{E}Idt \\&=+L\frac{d I}{d t}\cdot Idt=LIdI
\end{aligned}
The total work done in building up the current from 0 to $I_0$ is
\begin{aligned}
W&=\int d W =\int_0^{I_0} L I d I\\ &=L\left[\frac{I^2}{2}\right]_0^{I_0}=\frac{1}{2} L I_0^2
\end{aligned}
This work done is stored as the magnetic field energy $U$ in the inductor.
$$
\therefore \quad U=\frac{1}{2} L I_0^2
$$
Expression for average power stored in an inductor
Average power associated with an inductor. When a.c. is applied to an ideal inductor, the current lags behind the voltage in phase by $\pi / 2$ radian. So we can write the instantaneous values of voltage and current as follows :
\begin{aligned}
V &=V_0 \sin \omega t \\
\text { and } &=I_0 \sin \left(\omega t-\frac{\pi}{2}\right) \\
&=-I_0 \sin \left(\frac{\pi}{2}-\omega t\right)=-I_0 \cos \omega t \end{aligned}
Work done in small time $dt$ is
\begin{aligned} d W &=P d t=-V_0 I_0 \sin \omega t \cos \omega t d t \\
&=-\frac{V_0 I_0}{2} \sin 2 \omega t d t
\end{aligned}
The average power dissipated per cycle in the inductor is
| \begin{aligned} P_{a v} &=\frac{W}{T}=\frac{1}{T} \int_0^T d W \\ &=-\frac{V_0 I_0}{2 T} \int_0^T \sin 2 \omega t d t \\ &=+\frac{V_0 I_0}{2 T}\left[\frac{\cos 2 \omega t}{2 \omega}\right]_0^T=\frac{V_0 I_0}{4 T \omega}\left[\cos \frac{4 \pi}{T} t\right]_0^T \\ &=\frac{V_0 I_0}{4 T \omega}[\cos 4 \pi-\cos 0]=\frac{V_0 I_0}{4 T \omega}[1-1] \\ &=0 \end{aligned} |
Thus the average power dissipated per cycle in an inductor is zero.
Read Also
- Sharpness of Resonance: Q-Factor in LCR circuit, class 12
- Power in an AC circuit: definition, and formula derivation
- Choke coil – principle, working, and construction, class 12
- Resonance condition in a series LCR circuit
- Wattless current class 12
Frequently Asked Questions – FAQs
What is an inductor?
An inductor, a coil, choke, or reactor, is a two-terminal passive electrical component that stores energy in a magnetic field when an electric current is passed through it.
How is energy stored and released in an inductor?
The magnetic field surrounding an inductor stores energy as current flows through the field. If we slowly decrease the amount of current, the magnetic field begins to collapse and releases the energy and the inductor becomes a current source
Is the inductor an energy-storing device?
An inductor is an energy storage device that can be as simple as a single loop of wire or consist of many turns of wire wound around a core. Energy is stored in the form of a magnetic field in or around the inductor. Whenever current flows through a wire, it creates a magnetic field around the wire.
Why is the average power 0 in the inductor?
The average energy consumption per cycle in an inductor connected to a source is zero. The physical meaning of this result is as follows. During the first quarter of each current cycle, as the current increases, magnetic flux builds up through the inductor, and energy is stored in the inductor from the external source. In the next quarter cycle, as the current decreases, the flux decreases and the stored energy returns to the source. Therefore the inductor dissipates no net energy in a half cycle.
What is the unit of the inductor?
Henry (H)
Stay tuned with Laws Of Nature for more useful interesting content