GALILEANS & LORENTZ TRANSFORMATIONS | The basic mathematical operations for the special theory of relativity.

Today we are going to talk about a very important concepts that is the GALILEANS & LORENTZ TRANSFORMATIONS. And this concept of transformation is very important for the mathematical explaination of relativistic physics. When Einstein put his special theory of relativity in September 1905. Then various new concept get born out of this theory, that is the time dilatation, length contraction , mass energy equivalence, relativistic mass. And all this new concept can only be explained by using mathematics. So today we are going to take a look on this foundation mathematics of special theory of relativity, without which special theory of relativity is somehow incomplete.
So Let’s starts our talk with galilean transformation.

GALILEAN TRANSFORMATION

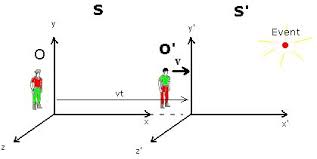
Consider the two frame of reference S and S’ having the coordinates of any point P is (x,y,z) and (x’,y’,z’) , initially both frame of reference are at same position ie. concide to each other, where t is zero for both reference when they are at initial stage. Then if second frame S’ starts moving in the direction of x – axis with some constant velocity v with respect to first frame of reference S. ( First frame is a fixed frame of reference).

Here you have to remember that this velocity is very very very small in comparison to speed of light. This is a day to day life velocity. Galilean Transformation is applicable only for small moving frame velocities.
If second frame is moving away from the fixed frame S with v velocity then the time elapsed for any observer which is present at fixed frame S will be t , but for observer which is in the moving frame will be t’.

And we know from above data that distance of point P from first frame S is x, and from second frame S’ is x’. Then the distance travelled by the second frame S’ wrt first frame S is given by the product of velocity v and time t ie. vt. ( Here v and t both are respect to S).
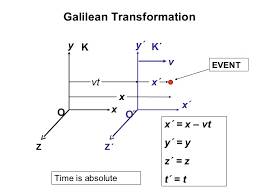
Then the distance between the point P and second frame S’ is given as difference of total distance from S ie. x and travelled distance ie.  vt ,.     x’ = x – vt.   if second frame S’ starts moving towards the fixed frame S, then total distance x is given as
x = x’ + vt’
And if S’ is moving along x axis only then y and z coordinates of point P is not changing, only x undergoes in changes because frame is moving along x axis. It means y’ = y and
z’ =z , and if velocity is very small then t and t’ will also same and there will be no difference in time.
Then the elements of fixed frame S is related to the elements of moving frame S’ is as follows.
x’ = x – vt , y’ = y , z’ = z , and t’ = t
This relationship is is called Transformation, and this Transformation is given by Galileo so it is called galilean transformation.
Now let’s talk about Lorentz Transformation

LORENTZ TRANSFORMATION

We have talked about the galilean transformation above , which is applicable only for small velocity. In which S’ is moving with small velocity v wrt fixed frame S.
But what would happen if second frame S’ starts moving with the approx of speed of light.
If it is moving with speed of light then difference between the t for fixed frame and t’ for moving frame is significant , because time becomes very very slow for moving frame wrt to fixed rest frame , which is called time dilation.

Now let’s talk about the Lorentz Transformation.
Consider the two frame of reference S and S’ having the coordinates of any point P is (x,y,z,t) and (x’,y’,z’,t’) , initially both frame of reference are at same position ie. concide to each other, where t is zero for both reference when they are at initial stage. Then if second frame S’ starts moving in the direction of x – axis with some constant velocity v with respect to first frame of reference S. And this velocity v is approximately equal to the speed of light,.    ( First frame is a fixed frame of reference).

 Now think that from a light source , a beam of light is to be focused on the point P from the origin of the fixed frame of reference S. And the same light beam is also focused on the point P from the origin of the moving frame of reference S’.
And we know from above data that distance of point P from first frame S is x, and from second frame S’ is x’.

Then these distances can also be expressed as :    x = ct , from the first frame of reference S, and x’ = ct’ , from the second frame of reference S’, which is moving.
x = ct
x’ = ct’
from the galilean transformation we know that ,.  x’ = x – vt , and  x = x’ + vt’
But in Lorentz Transformation this relation is written as :
x’ = k(x-vt)      and     x = k(x’+vt’)
Where k is some constant.
Multiplying these two  equations we get,
xx’ = k^2(x-vt)(x’+vt’).   Putting the value of x and x’ in the multiplication, we get,
c^2tt’ = k^2(ct-vt)(ct’+vt’)
c^2tt’ = k^2(c^2tt’ + cvtt’ -cvtt’ -v^2tt’)
c^2tt’ = k^2(c^2tt’-v^2tt’)
Then , k^2 = 1/[1- (v^2/c^2)]
And finally we get
k = 1/√[1- (v^2/c^2)] and this value of constant k is called Lorentz factor which is denoted by γ.
And  So ,.      γ = 1/√[1- (v^2/c^2)]
This is very important result , because it is very helpful to deriving the expression for time dilation , relativistic mass, length contraction. So this is all about THE GALILEAN & LORENTZ TRANSFORMATION.