Today we are going to talk about a very interesting concept of relativistic physics i.e. Length contraction. This concept is firstly postulated by George Fitzgerald and Hendrick Antoon Lorentz to explain the negative outcome of Michelson – Morley experiment and rescue the hypothesis of the stationary aether
But when Albert Einstein put his the special theory of relativity in September 1905.
Length contraction becomes a clear topic because this contraction can be easily explained by using the special theory of relativity.

The second postulate in the special theory of relativity says that the speed of light in the vacuum is constant for all observers, regardless of the motion of light source an observer, but you have to remember that any observable mass can’t travel with the speed of light.
but what would happen to the object which is moving with the speed of light? If an object is traveling with c then some physical dimensions of the object change.
The physical dimensions which go into change are its length. It is observed that when does object travels at a very high speed or with the speed of light, then the length of the object decreases.[latexpage]



Here an illustration is given to understand the length contraction phenomenon with different speeds. The first pic has normal speed, and the second pic has 80% of the speed of light, and the third pic is 99% of the speed of light.
You can clearly see the phenomenon of length contraction. Length contraction is the phenomenon in which the original length of the object decreases when they are traveling very fast.
This phenomenon is also known as Lorentz contraction or Lorentz Fitzgerald contraction. This contraction always occurs in the direction of the propagation of objects.
This effect is negligible at daily basis speeds but, This effect becomes more significant when they are traveling with the speed of light.
If length contraction occurred due to the increment in the object velocity in the direction of the motion. Then anyone can freely ask that why does length contraction phenomenon occur? Why does object length decreases if it is traveling at a very high speed?
We all know that length contraction is a true event, not an illusion but many of us think that it is a work of illusion. If it is not an illusion, then how can we explain it.
Undoubtedly its explanation is somehow complicated.
If we try to explain it theoretically without any use of the special theory of relativity, so here today we are going to explain it with the help of special relativity. Let’s begin…
SHOWING LENGTH CONTRACTION MATHEMATICALLY
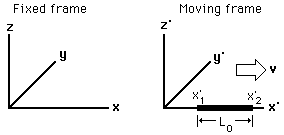
Let’s consider a two frame of reference S and S’, having coordinates (x,y,z) and (x’, y’,z’)
S’ frame is moving with a constant speed of velocity of v concerning frame S along the x-axis. A metal rod of length L0 which is its proper length put on the frame S’. If the frame is moving with v velocity then this rod is also moving with v velocity along the x-axis.
Let’s marked the two ends point of the rod as A and B. And if the distance of the point of A and B concerning the S frame is $x_1$ and $x_2$. Then their proper length can be given as $L_0=x_2-x_1$
And the distances of point A and B wrt to S’ frame is $x_1’$ and $x_2’$. And we know the object is moving with v which is very high then it suffers from length contraction. And the contracted length is given as L, which is given as $L = x_2′-x_1’$.
Now we have to use the Lorentz Transformation equation to find the relation between $x_1$ to $x_1’$ and $x_2$ to $x_2’$.
The general equation of relation is given as below.
$$x = \frac{(x’+ vt’)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}$$
Obtain the two relations by putting $x_1$ and $x_2$ in the above equation-
\begin{align*}
x_1& = \frac{(x_1’+ vt’)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}\\
x_2& = \frac{(x_2’+ vt’)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}
\end{align*}
Now subtract $x_1$ from $x_2$ to find the proper length of the rod.
\begin{align*}
L_0& = x_2-x_1\\
&=\frac{(x_2’+ vt’)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}-\frac{(x_1’+ vt’)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}
\end{align*}
If we solve it then the vt’ term gets canceled and a new equation will be.
$$L_0 = \frac{(x2′ – x1′)}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}$$
And we know that $x_2′-x_1’$ is equal to L which its contracted length. Then we get-
$$L_0 = \frac{L}{\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}$$
If we find for L then it becomes $$L =L_0\times {\sqrt{\left[1-\left(\frac{v^2}{c^2}\right)\right]}}$$ and here we clearly see that L is smaller than L0. This is the value of contracted length if it is traveling at a very high speed. If we put v = c in the above formula then we find that L becomes 0. Means objects having the speed of light then their length contracted to infinitely very small, which is somehow equal to zero, according to the equation.
