Nature Of Electromagnetic Waves, Class 12

From the humble light bulb to the latest 5G network, electromagnetic waves are all around us, shaping the way we communicate, navigate, and experience the world. Have you ever wondered how your phone can receive calls, how a microwave heats your food, or how radio broadcasts music to your car? The answer lies in the nature of electromagnetic waves. Electromagnetic waves are all around us, but what exactly are they, and how do they work?

In this day and age where we rely heavily on technology, understanding the nature of electromagnetic waves is more important than ever. Join me as we dive into the fascinating world of electromagnetic waves and uncover the nature of these invisible electromagnetic waves that shape our modern world.

Inside Story

What are electromagnetic waves?

Electromagnetic waves definition: Electromagnetic waves are a type of energy that travels through space in the form of oscillating electric and magnetic fields. They are produced by the movement of charged particles, such as electrons, and they can travel through a vacuum or through various materials.

Nature of electromagnetic waves, class 12 — Electromagnetic wave, source: Toppr

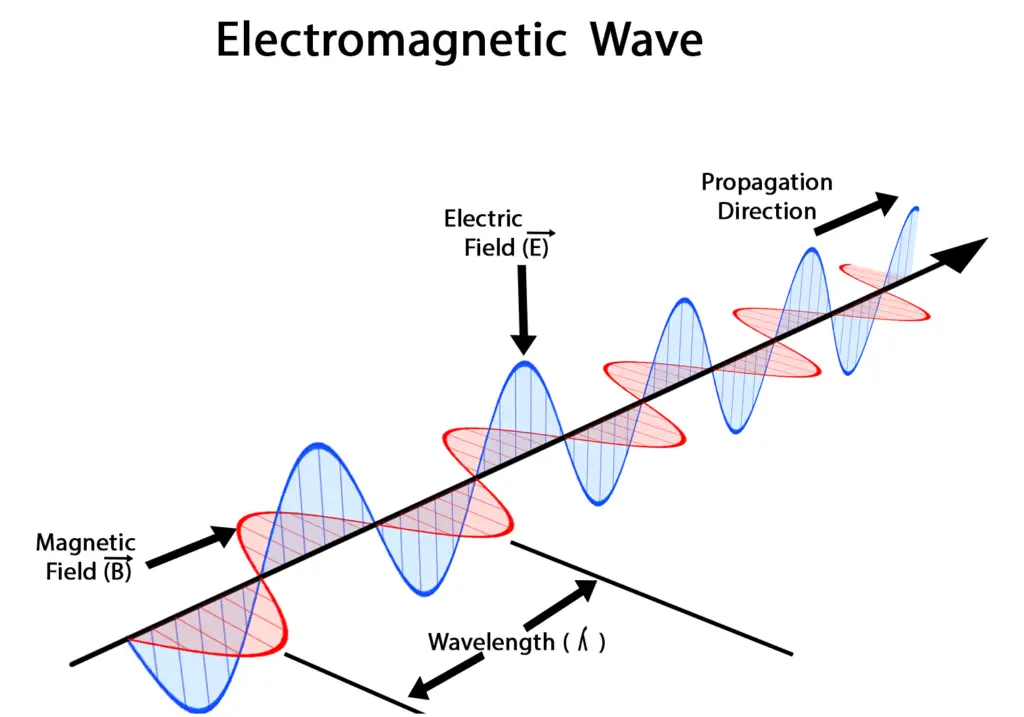
Electromagnetic waves include a range of frequencies, from low-frequency radio waves to high-frequency gamma rays, and they are responsible for many natural and man-made phenomena, including light, radio and television broadcasts, cell phone signals, X-rays, and more.

Read Also:

Electromagnetic waves class 12: definition, equation, graphical representation, and applications

Characteristics of electromagnetic waves, class 12

Electromagnetic waves are a type of wave that consists of two perpendicular waves oscillating together: an electric field and a magnetic field. These waves travel at the speed of light, and they can travel through a vacuum or through various materials, such as air, water, or even solid objects. Electromagnetic waves are produced by the movement of charged particles, such as electrons, and they can also be generated artificially using devices like antennas, lasers, or microwave ovens.

One of the key characteristics of electromagnetic waves is their frequency, which is the number of waves that pass by a given point in a given amount of time. The frequency of electromagnetic waves is measured in Hertz (Hz), which represents the number of cycles per second.

Electromagnetic waves with higher frequencies have more energy and shorter wavelengths, while waves with lower frequencies have less energy and longer wavelengths. This is why visible light, which has a higher frequency than radio waves, has a shorter wavelength and is able to penetrate solid objects like glass or water, while radio waves cannot.

Electromagnetic waves are also characterized by their amplitude, which is the height of the wave. The amplitude of an electromagnetic wave represents the strength of the electric and magnetic fields that are oscillating together. Waves with higher amplitudes have more energy and are able to cause greater changes in the matter they encounter.

Another important characteristic of electromagnetic waves is their polarization, which refers to the direction of the electric field as the wave travels through space. Polarization can be either linear or circular, depending on the orientation of the electric field. Linearly polarized waves oscillate in a single plane, while circularly polarized waves rotate as they travel.

Also, electromagnetic waves exhibit wave-particle duality, meaning they can act as both waves and particles. Photons, for example, are packets of energy that behave like both particles and waves, and they are responsible for the phenomenon of light. This duality helps explain why electromagnetic waves can sometimes behave like particles, such as when they are absorbed by matter, or like waves, when they diffract or interfere with each other.

Here are some key characteristics of electromagnetic waves:

Electromagnetic waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation.
They travel at the speed of light in a vacuum, which is approximately 299,792,458 meters per second.

Electromagnetic waves can have a wide range of frequencies, from low-frequency radio waves to high-frequency gamma rays.
The frequency of an electromagnetic wave determines its energy and its wavelength, with higher-frequency waves having more energy and shorter wavelengths.
Electromagnetic waves can be polarized, meaning that the direction of the electric field is fixed and oscillates in a single plane.
They can be absorbed, reflected, refracted, diffracted, and interfere with each other, depending on the properties of the medium they encounter.
Electromagnetic waves exhibit wave-particle duality, meaning they can act like both waves and particles (photons).
They are responsible for many natural and man-made phenomena, including light, radio, and television broadcasts, cell phone signals, X-rays, and more.

Electromagnetic waves can be used for communication, sensing, imaging, and many other applications.
The study of electromagnetic waves is essential for understanding and developing technologies that shape our modern world.

Read Also:

What are longitudinal waves?

Longitudinal waves are waves in which the particles of the medium vibrate or oscillate in a direction parallel to the direction of the wave’s propagation.

An example of a longitudinal wave is a sound wave, in which air molecules are compressed and expanded in the same direction as the wave travels. When a sound wave travels through air, for example, the air molecules in front of the wave are compressed, creating a region of high pressure, while the air molecules behind the wave are expanded, creating a region of low pressure.

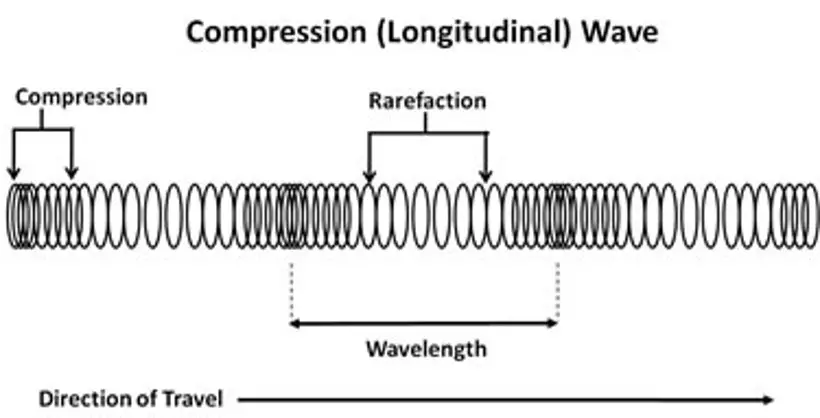
Other examples of longitudinal waves include seismic waves, which are waves that travel through the Earth’s interior during earthquakes, and pressure waves in fluids, such as the shock waves created by supersonic aircraft.

In contrast to transverse waves, which oscillate perpendicular to the direction of propagation, longitudinal waves oscillate parallel to the direction of propagation. This results in different properties and behaviors for longitudinal waves, such as the ability to compress and rarefy a medium, as well as the ability to be reflected, refracted, and diffracted.

What are transverse waves?

Transverse waves are waves in which the particles of the medium vibrate or oscillate in a direction perpendicular to the direction of the wave’s propagation.

An example of a transverse wave is a wave on a string, in which the particles of the string move up and down perpendicular to the direction of the wave’s motion. Another example is light waves, in which the electric and magnetic fields oscillate perpendicular to the direction of the wave’s propagation.

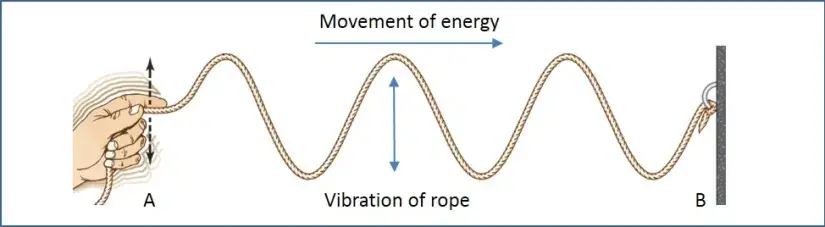
In transverse waves, the motion of the wave is perpendicular to the direction of energy transfer. This results in different properties and behaviors for transverse waves, such as the ability to be polarized, the ability to undergo interference and diffraction, and the ability to be reflected and refracted at interfaces between different media.

Transverse waves are different from longitudinal waves, in which the particles of the medium vibrate parallel to the direction of energy transfer. Examples of longitudinal waves include sound waves and seismic waves.

What is the nature of electromagnetic waves?

Electromagnetic waves are of transverse nature. Electromagnetic waves are a type of transverse wave that consists of electric and magnetic fields oscillating at right angles to each other and to the direction of the wave’s propagation.

They are produced by the motion of charged particles, such as electrons, and do not require a medium to propagate through, meaning they can travel through a vacuum.

The electric and magnetic fields in an electromagnetic wave are perpendicular to each other and to the direction of wave propagation, giving rise to a transverse nature. The strength of the electric and magnetic fields oscillate in a sinusoidal pattern, with the frequency of the oscillation determining the wavelength and energy of the electromagnetic wave.

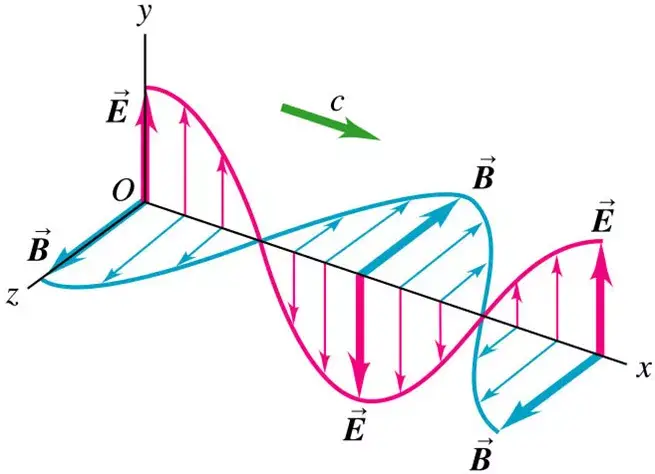
Electromagnetic waves can be described by their wavelength, frequency, and amplitude. Wavelength is the distance between two consecutive points on the wave that is in phase, or have the same degree of oscillation. Frequency is the number of complete oscillations of the wave that occur in one second, and it is measured in Hertz (Hz). Amplitude is the maximum displacement of the wave from its equilibrium position.

Electromagnetic waves are classified by their wavelength or frequency, with different regions of the electromagnetic spectrum corresponding to different types of waves. The electromagnetic spectrum includes radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays, with longer wavelength waves having lower frequencies and lower energy, and shorter wavelength waves having higher frequencies and higher energy.

Electromagnetic waves have a number of properties that distinguish them from other types of waves. For example, they are able to travel through a vacuum at the speed of light, meaning they do not require a medium to propagate through. They also have the ability to be polarized, meaning that the orientation of the electric and magnetic fields can be controlled.

Electromagnetic waves can be reflected, refracted, and diffracted when they encounter a boundary between two different media, and they can also undergo interference, resulting in constructive or destructive interference patterns.

The properties of electromagnetic waves make them useful in a wide range of applications, including communication technologies, such as radio and television broadcasting, cellular and satellite communications, and Wi-Fi networks. They are also used in medical imaging, such as X-rays and MRI scans, as well as in industrial processes, such as welding and heating.

Transverse nature of electromagnetic waves

Electromagnetic waves are transverse waves, meaning that the vibrations or oscillations of the wave occur perpendicular to the direction of propagation of the wave.

This is in contrast to longitudinal waves, such as sound waves, where the oscillations occur parallel to the direction of propagation.

In an electromagnetic wave, the electric and magnetic fields oscillate perpendicular to each other and to the direction of the wave’s motion. The electric field oscillates in one plane, while the magnetic field oscillates in a plane perpendicular to the electric field.

This perpendicular oscillation of the electric and magnetic fields creates a self-sustaining wave that can propagate through a vacuum, as well as through materials such as air, water, and solid objects.

The transverse nature of electromagnetic waves is fundamental to their properties and behavior, including their ability to travel at the speed of light, their polarization, and their ability to be reflected, refracted, and diffracted.

Transverse nature of electromagnetic waves proof

The transverse nature of electromagnetic waves can be proved in several ways. One of the most convincing proofs is through experiments that show the polarization of electromagnetic waves.

Polarization refers to the orientation of the electric and magnetic fields in an electromagnetic wave. If the electric and magnetic fields oscillate in a specific direction, the wave is said to be polarized in that direction. If the fields oscillate in all directions perpendicular to the direction of propagation, the wave is said to be unpolarized.

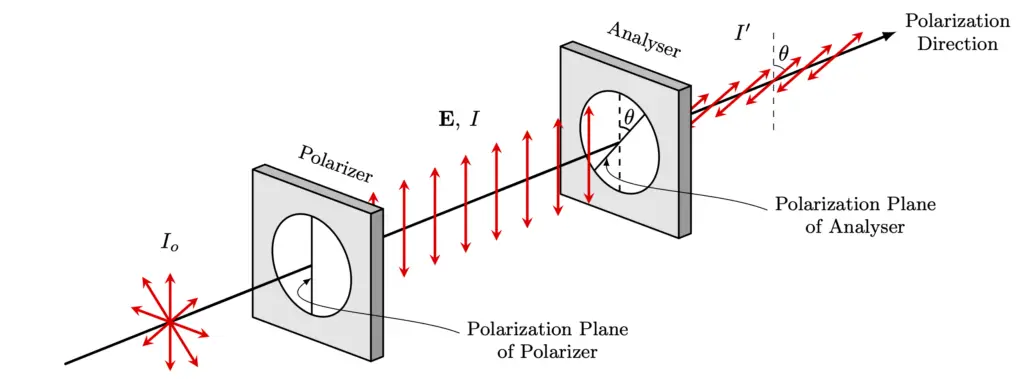
One experiment that demonstrates the transverse nature of electromagnetic waves is the Malus’ law experiment. In this experiment, a polarizing filter is used to polarize a beam of light. A second polarizing filter is then placed in the path of the polarized beam, and its orientation is gradually rotated. As the second filter is rotated, the intensity of the light passing through it decreases, until it becomes completely dark when the two filters are perpendicular to each other.

This phenomenon can only be explained if the light is transverse in nature. If light were longitudinal, the second filter would not affect the intensity of the light, regardless of its orientation. The fact that the intensity decreases as the second filter is rotated proves that the electric and magnetic fields are oscillating perpendicular to the direction of propagation.

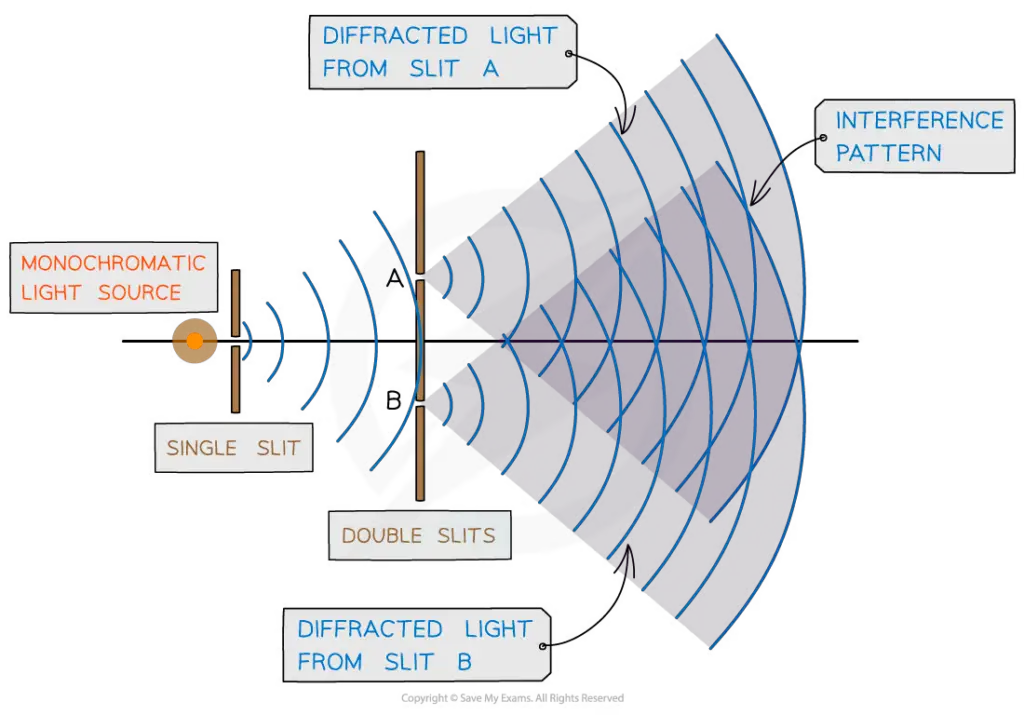
Another experiment that demonstrates the transverse nature of electromagnetic waves is the double-slit experiment. In this experiment, a beam of light is passed through two small slits and projected onto a screen. When the slits are close together, an interference pattern is observed on the screen, indicating that the light waves are interfering with each other. This interference pattern can only be explained if the light waves are transverse, with the electric and magnetic fields oscillating perpendicular to each other and to the direction of propagation.

So, experiments such as the Malus’ law experiment and the double-slit experiment provide strong evidence for the transverse nature of electromagnetic waves. These experiments demonstrate that electromagnetic waves have the ability to be polarized and that their oscillations occur perpendicular to the direction of propagation.

The transverse nature of electromagnetic waves can be observed and proven through various experiments, some of which are listed below:

Polarization of Light: When a light wave is polarized, its electric field vector vibrates only in one plane perpendicular to the direction of propagation. This indicates that light is a transverse wave.
Double-slit experiment: In this experiment, a beam of light is passed through two slits, and a screen is placed behind the slits to observe the interference pattern. The pattern shows that the electric and magnetic fields of the light waves are oscillating perpendicular to the direction of propagation, proving that they are transverse waves.

Faraday Rotation: In this experiment, a beam of linearly polarized light is passed through a transparent material in the presence of a magnetic field. The polarization plane of the light wave is rotated by an angle proportional to the strength of the magnetic field, indicating that the electric field is transverse.
Electromagnetic radiation from an accelerated charge: According to Maxwell’s equations, when an electric charge is accelerated, it produces electromagnetic radiation in the form of transverse waves.
Waveguide experiments: Waveguides are structures that are designed to guide and confine electromagnetic waves. The fact that the waves can be guided through narrow channels and can be reflected by surfaces perpendicular to the direction of propagation also supports the transverse nature of electromagnetic waves.

These experiments and observations provide strong evidence for the transverse nature of electromagnetic waves.

Another way to understand the transverse nature of electromagnetic waves is to consider the behavior of the wave in a medium. Electromagnetic waves can travel through a vacuum, but they can also travel through other media, such as air, water, or glass. When an electromagnetic wave enters a medium, it can interact with the charged particles in the medium, which can cause the wave to slow down, change direction, or even be absorbed.

The behavior of electromagnetic waves in a medium can be described by the refractive index of the medium, which is a measure of how much the wave slows down in the medium. The refractive index is related to the speed of light in the medium, which is given by:

\begin{align} v &= \frac{c}{n} \end{align}

where $c$ is the speed of light in a vacuum and $n$ is the refractive index of the medium.

In a medium, the electromagnetic wave can be decomposed into two orthogonal components, which are called the electric field and the magnetic field. These components are perpendicular to each other and to the direction of propagation of the wave. The electric field component is responsible for interacting with charged particles in the medium, while the magnetic field component is responsible for inducing currents in the medium.

If the electric field component of the wave is parallel to the surface of a medium, it can interact with the charged particles in the medium and cause them to oscillate in the same direction as the electric field. This interaction can lead to the absorption of the wave in the medium. However, if the electric field component of the wave is perpendicular to the surface of the medium, it cannot interact with the charged particles in the medium and is not absorbed.

Therefore, the fact that electromagnetic waves can propagate through a medium without being absorbed, as long as the electric field component is perpendicular to the surface of the medium, provides further evidence for the transverse nature of electromagnetic waves.

How to prove the transverse nature of electromagnetic waves mathematically?

The transverse nature of electromagnetic waves can be mathematically proven using Maxwell’s equations. Here is a simple proof:

Maxwell’s equations describe the behavior of electric and magnetic fields in space, and can be written in differential form as:

\begin{align} \nabla \cdot \mathbf{E} &= \frac{\rho}{\epsilon_0} \tag{1}\\ \nabla \cdot \mathbf{B} &= 0 \tag{2}\\ \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \tag{3}\\ \nabla \times \mathbf{B} &= \mu_0 \left(\mathbf{J} + \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right) \tag{4} \end{align}

where $\mathbf{E}$ is the electric field, $\mathbf{B}$ is the magnetic field, $\rho$ is the charge density, $\mathbf{J}$ is the current density, $\epsilon_0$ is the permittivity of free space, and $\mu_0$ is the permeability of free space.

Now, let’s consider a plane electromagnetic wave traveling in the $z$ direction with a frequency of $\omega$, a wavelength of $\lambda$, and an amplitude of $E_0$. We can express the electric and magnetic fields of the wave as:

\begin{align} \mathbf{E} &= \mathbf{\hat{x}} E_0 \cos(\omega t – k z) \tag{5}\\ \mathbf{B} &= \mathbf{\hat{y}} \frac{E_0}{c} \cos(\omega t – k z) \tag{6} \end{align}

where $\mathbf{\hat{x}}$ and $\mathbf{\hat{y}}$ are unit vectors in the $x$ and $y$ directions, respectively, $k = 2\pi/\lambda$ is the wave vector, and $c = 1/\sqrt{\epsilon_0\mu_0}$ is the speed of light in vacuum.

Now, let’s substitute equations (5) and (6) into equations (1)-(4) and see what happens. Starting with equation (1):

\begin{align} \nabla \cdot \mathbf{E} &= \frac{\rho}{\epsilon_0} \\ \frac{\partial E_x}{\partial x} &= 0 \tag{7} \end{align}

Equation (7) tells us that the $x$ component of the electric field does not vary with position, which is consistent with a transverse wave.

Next, let’s consider equation (2):

\begin{align} \nabla \cdot \mathbf{B} &= 0 \\ \frac{\partial B_y}{\partial y} &= 0 \tag{8} \end{align}

Equation (8) tells us that the $y$ component of the magnetic field does not vary with position, which is also consistent with a transverse wave.

Now, let’s consider equation (3):

\begin{align} \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\ \frac{\partial E_z}{\partial y} &= -\frac{1}{c}\frac{\partial B_y}{\partial t} \\ \frac{\partial E_z}{\partial y} &= -\frac{\omega}{c}B_0 \sin(\omega t – k z) \tag{9} \end{align}

where we have used the fact that $\frac{\partial B_y}{\partial t} = -\omega B_0 \sin(\omega t – k z)$, and $B_0 = \frac{E_0}{c}$ is the amplitude of the magnetic field.

Equation (9) tells us that the $z$ component of the electric field varies sinusoidally with position and time, which is consistent with a wave traveling in the $z$ direction.

Finally, let’s consider equation (4):

\begin{align} \nabla \times \mathbf{B} &= \mu_0 \left(\mathbf{J} + \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right) \\ \frac{\partial B_z}{\partial y} &= \mu_0 \epsilon_0 \frac{\partial E_z}{\partial t} \\ \frac{\partial B_z}{\partial y} &= -\frac{\mu_0\epsilon_0\omega}{c}E_0 \sin(\omega t – k z) \tag{10} \end{align}

Equation (10) tells us that the $z$ component of the magnetic field also varies sinusoidally with position and time, which is consistent with a wave traveling in the $z$ direction.

From equations (7), (8), (9), and (10), we can conclude that the electric and magnetic fields of a plane electromagnetic wave are both transverse to the direction of propagation. Therefore, we have mathematically proven the transverse nature of electromagnetic waves.

Read Also:

Stay tuned with Laws Of Nature for more useful and interesting content.

Was this article helpful?

YesNo