CONCEPTS OF PENDULUMS
Today we are going to talk about the various types of pendulums and their time periods. Pendulums play a very important role in simple harmonic motion physics that is also called oscillation.
So for everyone who reads and understands physics, it is necessary to understand the underlying concept of pendulums. So here we are going to cover a detailed talk on various types of pendulums. So stay tuned with us till the end. So let’s start…
First of all, we have to understand that, what is a pendulum? The pendulum is derived from the Latin word ‘pendulus‘ which means hanging.
So, a pendulum is nothing but it is only an arrangement in which, when weight is suspended from a pivot with an inextensible cord such that it can swing freely back and forth after applying a small force on the weight.
When no external force is applied in the bob, then the pendulum remains in the rest position. And the position where it remains in rest is called the mean position.
When a pendulum is swinging back and forth from its mean position then it gets displaced, and we see that after some time it comes to rest (mean position) Then from this, we can conclude that the mean position is applying some inward force, it is when, when bob swings away from the mean position.
And this inward force is called restoring force. It means we can say that always a restoring force is applied by the mean position on the bob, by which it comes in rest. And this restoring force is always directly proportional to the displacement of the bob from the mean position.
And this type of back and forth motion of pendulums in which restoring force, which is applied by the mean position, is always directly proportional to the displacement from the mean position is called oscillation or simple harmonic motion. All the pendulums which we are going to read, perform SHM, means oscillate about their mean position.
TYPES OF PENDULUMS
We are going to talk about four types of pendulums, which are listed below:
- Simple pendulum
- Compound or physical pendulum
- Conical pendulum
- Torsional pendulum
SIMPLE PENDULUM

A simple pendulum is also called a simple Gravitational pendulum, it is idealized simple pendulum consist of a weight (bob).
which is suspended by an inextensible and massless cord from a pivot having zero air drag and friction. If a small force is applied to the simple Gravitational pendulum, it will start oscillating with constant amplitude. But when Normal pendulums or real pendulums start oscillating back and forth.[latexpage]
Its motion is hindered by the air drag and friction, by which its amplitude gradually declines. Practically it is not possible to make an ideal simple pendulum. So for practical uses, a simple pendulum is obtained by suspending a weight (bob) with a fine cotton thread from a pivot.
DERIVATION FOR TIME PERIOD OF A SIMPLE PENDULUM

We have to understand the meaning of time period-
the time period is nothing but it is only the time taken by the bob to complete one full oscillation.
Now, consider an ideal simple pendulum, having bob of mass m, and hangs with a massless and inextensible cord of length L, and the other end of the cord is fixed to a pivot, as shown above. Now, think that this pendulum is swinging back and forth and you stop it at any instant of oscillations.
At any instant of the stoppage of the pendulum, we find that θ is the angular displacement which is made by the bob from the mean position. $W = mg$ is the weight that is acting towards the ground and balance by the normal reaction $R$, $R = W = mg$, and θ is the angle between the cord and the normal reaction. After resolving the mg in X and Y components, we get $-mgsin\theta$ along X-axis and $-mgcos\theta$ along Y-axis. $-mgsin\theta$ acts as restoring force, because during oscillations this force pulls the bob towards the mean position.
Minus sign is because this force acts in the opposite direction of the motion of the bob. And $-mgcos\theta$ is acted along the cord but in the opposite direction of the tension in the cord.$$T = -mgcos\theta$$
and restoring force $$F = -mgsin\theta$$.
Restoring force (F) is perpendicular to the length of the cord(L), and we know that torque τ is $\displaystyle{r \times F = rFsin\theta}$, here r is length L and force is $mgsin\theta$. Then τ is given as $mgsin\theta L$
$$\tau = -mgLsin\theta = I\alpha $$
where I is moment of inertia and α is angular acceleration.
If θ is very small then $sin\theta = \theta$
\begin{align*}
\tau& = -mgL\theta =I\alpha\\
\text{then},\; I\alpha = -mgL\theta\\
\alpha & = \left(\frac{-mgL}{I}\right)\theta
\end{align*}
equating with $a = -\omega^2x$
$$-\omega^2 = \frac{-mgL}{I}\;\text{(minus minus get cancelled)}$$
$$\omega = \sqrt{\left(\frac{mgL}{I}\right)}$$
We know that $\displaystyle{\omega = \frac{2\pi}{T}}$ then we get-
$$\frac{2\pi}{T} = \sqrt{\left(\frac{mgL}{I}\right)}$$
$$T = 2\pi\sqrt{\left(\frac{I}{mgL}\right)}$$
Moment of inertia of bob is $mL^2$, putting it into the above expression, we get-
$$T = 2\pi\sqrt{\left(\frac{mL^2}{mgL}\right)}$$
$$T = 2\pi\sqrt{\left(\frac{L}{g}\right)}$$
This is the required time period of the simple pendulum.
But this formula is not general, the general formula for the time period of a simple pendulum is-
$$T = 2\pi\sqrt{\frac{RL}{g(R+L)}}$$
where R is the radius of the earth and L is the length of the pendulum.
RESULTS TO BE NOTED
- If the angular amplitude of the simple pendulum is more, then the time period is $$T = 2\pi\sqrt{\left(\frac{L}{g}\right)}\times \left(1+\frac{{\theta}^2}{16}\right)$$ where θ is in radians.
- On an increasing length of a simple pendulum, the time period increases, but the time period of a simple pendulum of infinite length is 84.6 minutes, which is maximum and is equal to the- $$T = 2\pi\sqrt{\frac{R}{g}}$$
- If the time period of the clock based on the simple pendulum increases, then click will be slow, but if the time period decreases then the clock will be fast. If g remains constant and ∆l changes in length, then- $$\left(\frac{\Delta T}{T}\right)\times 100 = \left(\frac{\Delta l\times 100}{2l}\right)$$
- If l remains constant and ∆g changes in acceleration, then- $$\left(\frac{\Delta T}{T}\right)\times 100 = -\left(\frac{\Delta g\times 100}{2g}\right)$$
- If both length and acceleration is changes by ∆l and ∆g then,- $$\left(\frac{\Delta T}{T}\right)\times 100= \frac{1}{2}\left[\left(\frac{\Delta l}{l}\right)-\left(\frac{\Delta g}{g}\right)\right]\times 100$$
Now we are going to talk about the physical pendulum or compound pendulum.
COMPOUND PENDULUM AND ITS TIME PERIOD
When a rigid body is suspended from one axis and made to oscillates about it, then this type of pendulum is called compound or physical pendulum. See below;

CONICAL PENDULUM
For reference see below;
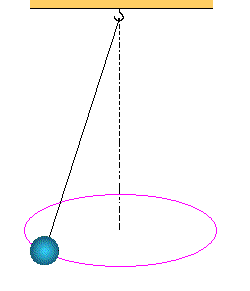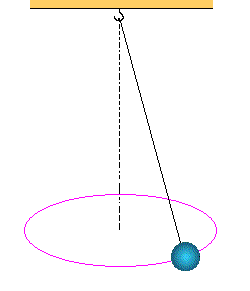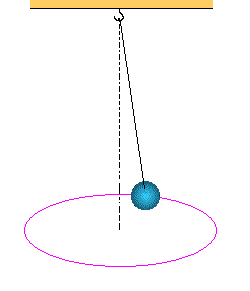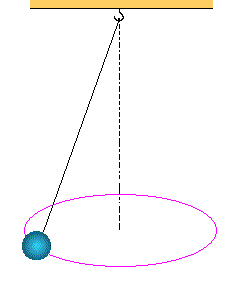
DERIVATION OF TIME PERIOD OF CONICAL PENDULUM
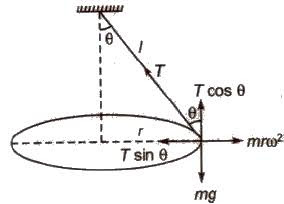
Let’s consider the T is the tension in the string and L is the length of the string, and r is the radius is the cone, which is made by the horizontal circular motion of the string. And h is the height of the cone. m is the mass of the bob.
TORSIONAL PENDULUM AND ITS TIME PERIOD
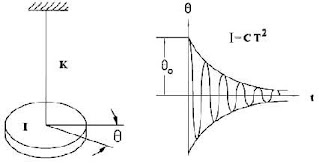
First of all, we have understood the meaning of torsion. Have you ever twist any flexible grass or rubber objects. What do you see, you must have seen that after twisting it many times it again comes to its original condition, or it tends to come in its original position.
This means when we applied a force to twist and after releasing the twisting force, an opposite force is applied to regain its original condition. This is called torsion, and the pendulum which works on this concept called the torsional pendulum.
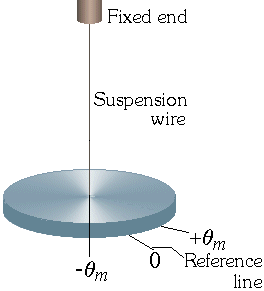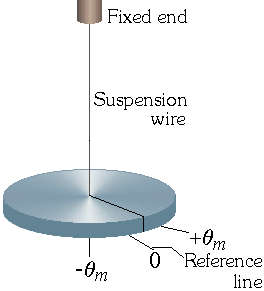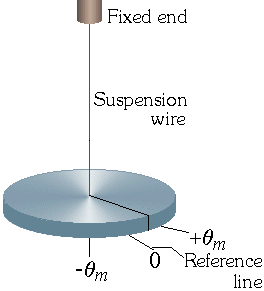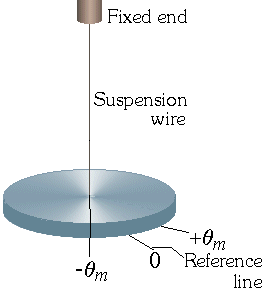
This is required time period of torsional pendulum.


