So today we are going to talk about a very important and interesting concept of hydrodynamics i.e equation of continuity.

Ask yourself this question:

• What is the mean of continuity?
• And why are we using it here is hydrodynamics?

Continuity means anything which covers equal displacement in an equal time interval.

In fluid mechanics, if V volume of liquid is entering in ∆t then the same volume of liquid is exiting in ∆t also.

Fluid has so many properties, but the property by which it became unique, is the property of incompressible, it means fluid can’t be compressed by any means,
Here fluid means liquid.

In hydrodynamics, we consider an ideal fluid,  because mathematical modeling of real fluid is very complicated.
An ideal fluid is that fluid that is non-viscous, incompressible, and irrotational.

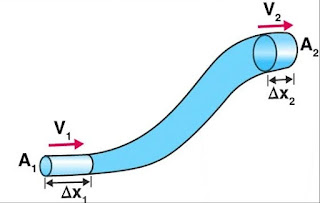
So it is observed that when an ideal fluid flows through the pipe of different cross-sectional areas, the volume of fluid that is entering is equal to the volume of fluid which is an exit.

If the fluid is ideal then its density is constant at every point. If the volume is equal and its density is constant then the mass of fluid that is entering is also equal to the mass of fluid that is coming out.[latexpage]
$$
V = \frac{m_1}{\rho} = \frac{m_2}{\rho}\qquad   \text{then} \qquad  m_1 = m_2$$
Conservation of mass is applying here.

DERIVATION FOR EQUATION OF CONTINUITY

Let’s take a pipe of different cross sectional area with one end have $A_2$, $v_2$ ,∆t ,$P_2$ ,$\rho_2$ and at second end $A_1$ , $v_1$, ∆t, and $P_1$, $\rho_1$.
Here ∆t is a small-time interval in which fluid gets displaced. And $\rho_1 =\rho_2$ due to ideal nature of fluid.

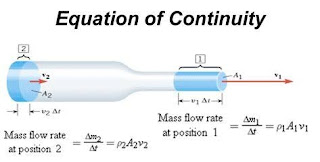
We know that mass of fluid that is entering is equal to the mass of fluid that is coming out, so $m_2 = m_1$
And $m_2=V\rho_2$ , and $m_1 = V\rho_1$. Then we can say that $V\rho_2=V\rho_1$
Then, the Volume is given as-
$$
V =\text{cross sectional area}\times \text{displacement}
$$
So, $V=A_2v_2\Delta t$ and $V=A_1v_1\Delta t$
Putting value we get-
$$
A_2v_2\Delta t\rho_2=A_1v_1\Delta t\rho_1$$
But $\rho_2=\rho_1$ So, we get after canceling ∆t and ρ both side
$$
V = A_1v_1 = A_2v_2 = \text{constant}
$$
This equation is called the equation of continuity. Watch this video for more reference.