Physical and chemical properties of matter
In our surroundings, there are large numbers of matter. A matter is nothing but the materials that have mass and occupy some space by their volume. Every matter that you see in your surroundings has some unique properties and characteristics that make them different from each other.
These properties of matter can be classified into two categories —
- Physical properties, such as colour, odour, melting point, boiling point, density, etc., and
- Chemical properties, like composition, combustibility, ractivity with acids and bases, etc.
Physical properties can be measured or observed without changing the identity or the composition of the substance. This means physical changes do not affect the identity and composition of the matter.
But the measurement or observation of chemical properties requires a chemical change to occur whereas measurement of physical properties does not require the occurrence of a chemical change. The examples of chemical properties are characteristic reactions of different substances; these include acidity or basicity, combustibility, etc.
The chemist uses these properties of matter (physical or chemical properties) to predict the behavior of the matter, which is determined by careful measurements and experimentation.
Suggested reading: Physical and chemical properties of matter chemistry class 11
In this article, we will discuss the measurements of physical properties of matter quantitatively, so let’s get started… [latexpage]
Measurements of physical properties of matter quantitatively
Why do we need to measure the physical properties of matter quantitatively? We need it because quantitative measurements of physical properties are required for scientific research. Many properties of matter, such as length, area, mass, volume, etc., are quantitative in nature because they can be measured by mathematical operations.
It all can be measured by a numeric value by using a preferred suffix called unit. Any quantitative observation or measurement is represented by a number followed by units in which it is measured. For example, the mass of a ball can be represented as 10 kg; here, 10 is the number and kg denotes kilograms, the unit in which the mass of the ball is measured.
So for the measurements of physical properties of matter quantitatively two different systems of measurement have been developed that is:
- English or British System (FPS system) and
- Metric System (MKS system)
Both measurement systems were being used in different parts of the world. The metric system, which was originated in France in the late eighteenth century, was more convenient than other measuring systems because it was based on the decimal system.
Suggested reading: Matter | Nature of matter | classification of matter, class 11 | some basic concepts of chemistry
But further, a need for a universal standard system was felt by the scientific community. So in this regard, a universal standard system was established in 1960, which is known as the international system. We will discuss more it below.
The international system of units (SI system)
The international system of units (in French, it is Le Systeme International d’Unités — abbreviated as SI) was established by the 11th General Conference on Weights and Measures (in French Conference Generale des Poids et Measures abbreviated as CGPM). CGPM is an inter-governmental treaty organization created by a diplomatic treaty known as the meter convention, which was signed in Paris in 1875.
In the SI system of units, there are seven base units called fundamental units. These fundamental units pertain to the seven fundamental physical quantities. Other physical quantities such as speed, density, acceleration, etc are called derived physical quantities because their units can be derived by the seven base units. Fundamental physical quantities along their base units are listed in the table be below:
| Fundamental physical quantities | Symbol for quantities | Name of the SI unit | The symbol for the SI unit |
| Length | l | meter | m |
| Mass | m | kilogram | kg |
| Time | t | second | s |
| Electric current | I | ampere | A |
| Thermodynamic temperature | T | kelvin | K |
| Amount of substance | n | mole | mol |
| Luminous intensity | Iv | candela | Cd |
The definition of each base quantity is given in the table below:
| Fundamental physical quantities | Name of the physical quantity | Definition of the quantity |
| Length | meter | It is the distance traveled by the light in 1/299792458 seconds. |
| Mass | kilogram | The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of c and ΔνCs. |
| Time | second | One second is defined as “9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom |
| Electric current | ampere | The ampere is defined by taking the fixed numerical value of the elementary charge e to be 1.602 176 634 × 10−19 when expressed in unit C, which is equal to A.s, where the second is defined in terms of ∆νCs, the unperturbed ground-state hyperfine transition frequency of the cesium-133 atom |
| Thermodynamic temperature | kelvin | The kelvin is now defined by fixing the numerical value of the Boltzmann constant k to 1.380649×10−23 J⋅K−1. Hence, one kelvin is equal to a change in the thermodynamic temperature T that results in a change of thermal energy kT by 1.380649×10−23 J |
| Amount of substance | mole | It is defined as exactly 6.02214076×1023 elementary entities (“particles”), which may be atoms, molecules, ions, or electrons. |
| Luminous intensity | candela | One candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 × 1012 Hz and that has a radiant intensity in that direction of 1/683 watt per steradian |
In SI unit some prefixes are used to denote the multiple and sub-multiple of a unit. The prefixes used in the SI unit are listed in the table below:
| Multiple | Prefix | Symbol |
| 10-24 | Yocto | y |
| 10-21 | Zepto | z |
| 10-18 | Atto | a |
| 10-15 | Femto | f |
| 10-12 | Pico | p |
| 10-9 | Nano | n |
| 10-6 | Micro | μ |
| 10-3 | Mili | m |
| 10-2 | Centi | c |
| 10-1 | Deci | d |
| 10 | Deca | da |
| 102 | Hecto | h |
| 103 | Kilo | k |
| 106 | Mega | M |
| 109 | Giga | G |
| 1012 | Tera | T |
| 1015 | Peta | P |
| 1018 | Exa | E |
| 1021 | Zeta | Z |
| 1024 | Yotta | Y |
Mass and weight
Every substance has a mass in it, if they have mass then they have also weight. Mass is the amount of matter present in it but weight is the force exerted by gravity. The mass of a substance is a constant quantity. It does not vary if position changes, wherever you put the substance in this whole universe, its mass can’t be changed.
But on the other hand weight (derived physical quantity) is a variable quantity, it varies from place to place because the acceleration due to gravity varies from place to place. If someone’s weight on the earth is 50N then the weight of that person will be different on the other planets because every planet has a different acceleration due to gravity.
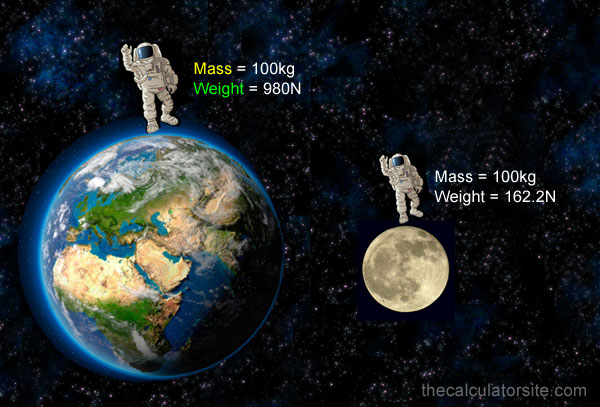
The SI unit of mass from the table above is Kilograms (Kg) and the unit of weight is Newton (N).
Volume
Volume is the space occupied by the substance. Its unit is m3 (length)3. In laboratories, the volume of liquids or solutions can be measured by graduated cylinder, burette, pipette, etc. A volumetric flask is used to prepare a known volume of a solution. Some measuring devices are shown below:
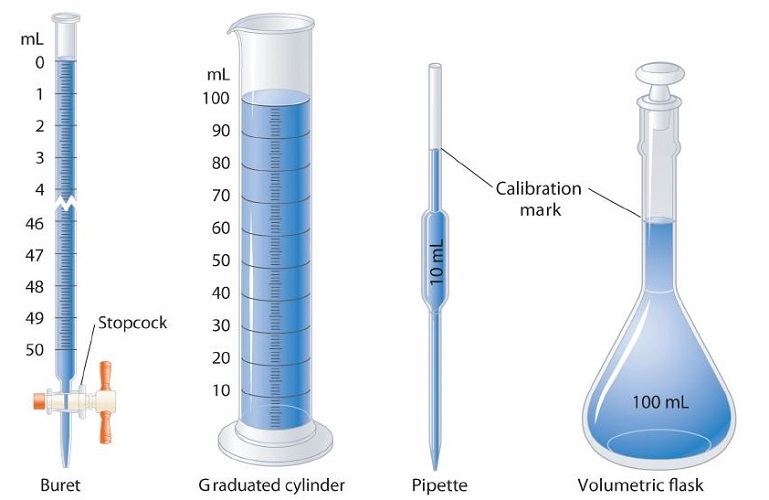
Density
The density of any substance is related to mass and volume is as follows: $$\text{Density}=\frac{\text{Mass}}{\text{Volume}}$$ Density of any substance is defined as the amount of mass per unit volume. It is given as below:
| $$\text{SI unit of density}=\frac{\text{SI unit of mass}}{\text{SI unit of volume}}$$ $$=\frac{kg}{m^3}=Kg.m^{-3}$$ |
This unit of density is very large so chemists often use a smaller version of density i.e g/cm³, where mass is expressed in grams (g) and length is expressed in centimeters (cm). Density is quite useful for analyzing the packaging of matter constituents. It tells that how closely the particles of matter are packed. If the density is larger then it means particles are packed more closely.
Temperature
Temperature is a physical quantity that measures the hotness and coldness of any substance. There are three common scales to measure the temperature of any object i.e °C (degree Celsius), °F (degree Fahrenheit), and K (Kelvin). Here, K is the SI unit of temperature.
The thermometer with the Celsius scale is calibrated from 0°C to 100°C. On the Celsius scale, 0°C is the freezing point and 100°C is the boiling point of water. The thermometer with the Fahrenheit scale is calibrated between 32°F to 212°F.
The temperature of Celsius and Fahrenheit scale is related with the following formula: $$^{\circ} F=\frac{9}{5}^{\circ}C +32$$
The relation between Celcius and Kelvin scale is given as below: $$K=^{\circ}C +273.15$$ Thermometer based on these three scales is given below:
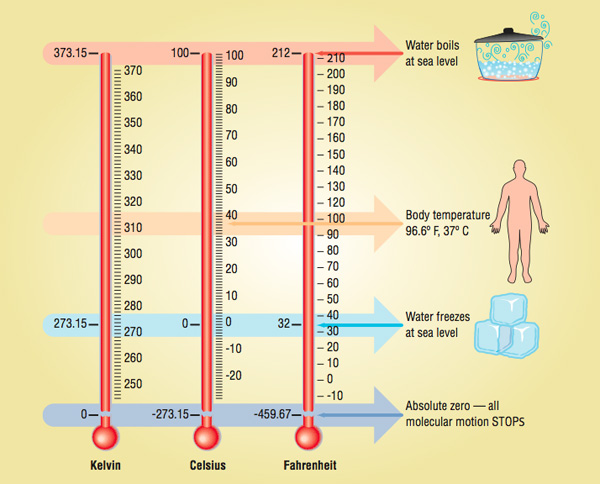
| Note – Temperature below 0°C (negative temperature) is possible on the Celcius scale but on the Kelvin scale, the negative temperature cannot exist. |
Stay tuned with Laws Of Nature for more useful and interesting content.



