Inside Story
-
1 THREE DIMENSIONAL GEOMETRY
- 1.1 ORIGIN
- 1.2 COORDINATE AXES
- 1.3 COORDINATE PLANES
- 1.4 COORDINATES
- 1.5 DISTANCE FORMULA
- 1.6 VECTOR FORM
- 1.7 DIRECTION COSINES
- 1.8 STRAIGHT LINES
- 1.9 SKEW LINES
THREE DIMENSIONAL GEOMETRY
ORIGIN
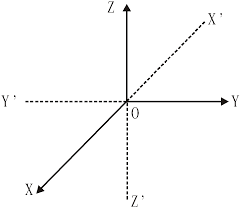
In the following diagram X’OX , Y’OY and Z’OZ are three mutually perpendicular lines , which intersect at point O. Then the point O is called origin.
COORDINATE AXES
In the above diagram X’OX is called the X axes, Y’OY is called the Y axes and Z’OZ is called the Z axes.
COORDINATE PLANES
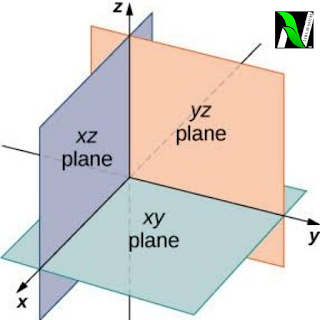
1). XOY is called the XY plane.
2). YOZ is called the YZ plane.
3). ZOX is called the ZX plane.
If all these three are taken together then it is called the coordinate planes.
These coordinates planes divides the space into 8 parts and these parts are called octants.
COORDINATES
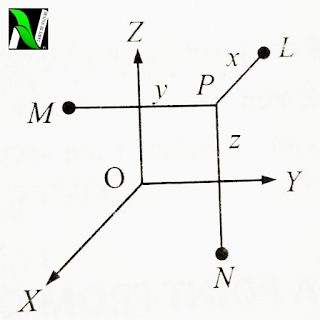
Let’s take a any point P in the space. Draw PL , PM and PN perpendicularly to the XY, YZ and ZX planes, then
1). LP is called the X – coordinate of point P.
2). MP is called the Y – coordinate of point P.
3). NP is called the Z – coordinate of the point P.
When these three coordinates are taken together, then it is called coordinates of the point P.
SIGN CONVENTION OF A POINT
The sign of the coordinates of a point in the space is depends on the motion of the point.
If the point is moving along or parallel to the OX, OY and OZ then it will be positive. But if it is moving along or parallel to the OX’ , OY’ and OZ’ then it will be negative.
POINTS TO BE REMEMBERED |
|
1). The coordinates of any point on the X axes are of the form of (a,0,0) , similarly for the Y and Z axes is (0,b,0) and (0,0,c).
2). Coordinates of any point in the XY plane is given as (a,b,0) , similarly for YZ and ZX planes are (0,b,c) and (a,0,c). 3). The equation of the XY plane is given as z = 0, similarly for YZ plane is x = 0 and for ZX plane is y = 0. |
DISTANCE FORMULA
DISTANCE FORMULA
The distance between the two points A ( x1, y1, z1) and B ( x2, y2, z2) is given as-
AB = √[(x2 -x1)^2 + (y2 -y1)^2 + (z2 -z1)^2]
DISTANCE FROM THE ORIGIN
If O is origin and P (x,y,z) is any point in the space then, the distance of point P from the origin is –
OP = √(x^2 + y^2 + z^2)
POINTS TO BE REMEMBERED |
|
1). The position vector r of any point P (x,y,z) is given as r = xî+yĵ+zk̂ , conversely if position vector r is given as r = xî+yĵ+zk̂ then , it’s point of coordinate is P(x,y,z).
2). The distance of any point P (x,y,z) from the origin O is given as √(x^2 + y^2 + z^2). It is equivalent to the |OP| vector. |
DISTANCE OF A POINT FROM THE COORDINATE AXES
If P (x,y,z) is any point in the space and PA , PB and PC be perpendiculars drawn from point P to the axes OX , OY and OZ respectively. Then
PA = √(y^2 + z^2)
PB = √(z^2 + x^2)
PC = √(x^2 + y^2)
SECTION FORMULA
The coordinates of the point dividing the line joining the point P(x1,y1,z1) and Q(x2,y2,z2) in the ratio of m:n internally is given by-
[(mx2+nx1)/(m+n) , (my2+ny1)/(m+n) , (mz2+nz1)/(m+n)]
The coordinates of the point dividing the line joining the point P(x1,y1,z1) and Q(x2,y2,z2) in the ratio of m:n externally is given by-
[(mx2-nx1)/(m-n) , (my2-ny1)/(m-n) ,
(mz2-nz1)/(m-n)]
The coordinates of the mid point of points (x1,y1,z1) and (x2,y2,z2) is –
[(x1+x2)/2 , (y1+y2)/2 , (z1+z2)/2]
VECTOR FORM
INTERNAL DIVISION
If the point R divides the line joining the point P and Q internally in the ratio of m:n then , the position vector R(r) is given by-
r = (mr2 + nr1)/(m+n)
EXTERNAL DIVISION
If the point R divides the line joining the point P and Q externally in the ratio of m:(-n) then , the position vector R(r) is given by-
r = (mr2 – nr1)/(m-n)
MID POINT
If the R is the mid point of the line joining the point PQ , then, m:n = 1:1 , then the position vector R(r) is –
r = (r1+r2)/2
COORDINATES OF THE GENERAL POINT
The coordinates of any point which are lying on the line joining the points P(x1,y1,z1) and Q(x2,y2,z2) is given by-
[(kx2+x1)/(k+1) , (ky2+y1)/(k+1), (kz2+z1)/(k+1)]
CENTROID OF A TRIANGLE
The centroid of a triangle ∆ABC whose vertices are A(x1,y1,z1) , B(x2,y2,z2) and C(x3,y3,z3) are –
[(x1+x2+x3)/3 , (y1+y2+y3)/3 , (z1+z2+z3)/3]
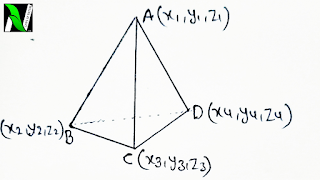
CENTROID OF A TETRAHEDRON
The centroid of a tetrahedron, whose vertices are A(x1,y1,z1) , B(x2,y2,z2) ,C(x3,y3,z3) and D(x4,y4,z4) are given as-
[(x1+x2+x3+x4)/4 , (y1+y2+y3+y4)/4 , (z1+z2+z3+z4)/4]
DIRECTION COSINES
If a line makes angle α , β and γ with positive directions of x,y and z axes then, cosα , cosβ and cosγ are called the direction cosines.
Generally direction cosines are denoted by l , m and n. ie. l = cosα , m = cosβ and n = cosγ
And the angles α , β and γ are called direction angles.
DIRECTION RATIOS
The three number a, b and c which are proportional the direction cosines l, m and n of the line are called direction ratios of the line.
l = ak , m = bk , n = ck , where k is any constant.
USEFUL RESULTS ON DIRECTION COSINES AND DIRECTION RATIOS
Let any point P(x,y,z) in the space such that
r = OP has direction ratios l, m and n , then.
1). x = l|r| , y = m|r|, z = n|r|
2). l|r| , m|r|and n|r| are the projection of r on the OX, OY and OZ respectively.
3). r = |r|(lî+mĵ+nk̂) or r^ = lî+mĵ+nk̂
4). l^2 + m^2 + n^2 = 1
5). If r = aî+bĵ+ck̂ then,
a, b and c are the direction ratios of r.
Direction cosines of r can be given as –
l = a/√(a^2+b^2+c^2)
m = b/√(a^2+b^2+c^2)
n = c/√(a^2+b^2+c^2)
6). Direction ratios of the line joining the point P(x1,y1,z1) and Q(x2,y2,z2) are (x2-x1), (y2-y1),(z2-z1) and it’s direction cosines are
x2-x1/|PQ| , y2-y1/|PQ| , z2-z1/|PQ|
7). Direction cosines of
OX = (1,0,0)
OY = (0,1,0)
OZ = (0,0,1)
DANGER |
| 1). The direction cosines of a line is unique but it’s direction ratios need not to be unique, it can be infinite. |
ANGLES BETWEEN TWO LINES
If the two lines of directions cosines are (l1,m1,n1) and (l2,m2,n2) and θ is the angle between the lines. then,
Cosθ = l1l2+m1m2+n1n2 and
Sinθ = √[(m1n2-m2n1)^2 +(n1l2-n2l1)^2 +(l1m2-l2m1)^2]
POINTS TO BE REMEMBERED |
|
1). If l1l2+m1m2+n1n2 = 0 then , the two vectors r1 and r2 having direction cosines l1,m1,n1 and l1,m2,n2 are orthogonal.
2). If l1/l2 = m1/m2 = n1/n2 are equal then the two vectors are parallel. 3). If a vector is equally inclined to the axes then the direction cosines are 4). If a line make α , β , γ and δ with the four diagonal of the cube then. 5). Angle between the any two diagonal of cube is cos-1(1/3). 6). Angle between the diagonal of the cube and the diagonal of the face is cos-1[√(2/3)]. |
ANGLES IN TERMS OF DIRECTION RATIOS
If the direction ratios of the two lines are (a1,b1,c1) and (a2,b2,c2) and θ is the angle between them, then-
Cosθ = (a1a2+b1b2+c1c2)/√(a1^2+b1^2+c1^2).√(a2^2+b2^2+c2^2)
POINTS TO BE REMEMBERED |
| If two lines are perpendicular then a1a2+b1b2+c1c2 = 0 , and if they are parallel then, a1/a2=b1/b2=c1/c2 |
PROJECTION
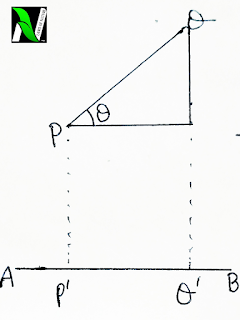
The projection of a line joining the point P(x1,y1,z1) and Q(x2,y2,z2) on the another line P’Q’ whose direction cosines are l , m and n and the line PQ makes angle θ with the line P’Q’.
Then, the projection of the line PQ is given as-
The projection of PQ is P’Q’ = PQcosθ
= (x2-x1)cosα +(y2-y1)cosβ +( z2-z1)cosγ
= (x2-x1)l +(y2-y1)m +( z2-z1)n
STRAIGHT LINES
EQUATION OF THE LINE PASSING THROUGH A POINT AND PARALLEL TO A GIVEN VECTOR
VECTOR FORM
The vector equation of the straight line passing through a point a and which are parallel to a given vector b is –
r = a + λb
Where λ is a scalar quantity.
CARTESIAN FORM
The equation of the straight line having direction ratios a,b and c and passing through a fixed point (x1,y1,z1) is –
(x-x1)/a = (y-y1)/b = (z-z1)/c
POINTS TO BE REMEMBERED |
|
1). The position vector of any point on the line is taken as = a+λb
2). If r is a position vector of any point P (x,y,z) then, r = xî+yĵ+zk̂ 3). Equation of the line whose direction cosines are l,m and n and passing through a fixed point (x1,y1,z1) is – (x-x1)/l =(y-y1)/m = (z-z1)/n 4). The coordinates of any point on the line (x-x1)/a = (y-y1)/b = (z-z1)/c is given as 5). The equation of X axes is *. Equation of y axes is *. Equation of z axes is |
EQUATION OF THE LINE PASSING THROUGH TWO POINTS
VECTOR FORM
The vector equation of the line passing through the two points having position vector a and b is-
r = a + λ(b – a)
CARTESIAN FORM
The Cartesian equation of the line passing through the two given points (x1,y1,z1) and (x2,y2,z2) is –
(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1)
CHANGING UNSYMMETRICAL FORM TO SYMMETRICAL FORM
The unsymmetrical form of line
ax + by + cz +d = 0 and ax’+ by’+cz’+d’ = 0 can be changed to symmetrical form is as follow –
ANGLES BETWEEN THE LINES
VECTOR FORM
The angles between the two lines
r = a1 + λb1 and r = a2 + μb2 is given as –
Cosθ = b1.b2/|b1||b2|
CARTESIAN FORM
The angles between the two lines having Cartesian equation
(x-x1)/a1 = (y-y1)/b1 = (z-z1)/c1 and
(x-x2)/a2 = (y-y2)/b2 = (z-z2)/c2 is given as-
Cosθ = (a1a2+b1b2+c1c2)/√(a1^2+b1^2+c1^2).√(a2^2+b2^2+c2^2)
INTERSECTION OF TWO LINES
If the two given lines are
(x-x1)/a1 = (y-y1)/b1 = (z-z1)/c1 and
(x-x2)/a2 = (y-y2)/b2 = (z-z2)/c2
TO FIND THE POINT OF INTERSECTION
STEP(1): write the coordinates of the general points of both lines equation as follow-
(x-x1)/a1 = (y-y1)/b1 = (z-z1)/c1 = λ
(x-x2)/a2 = (y-y2)/b2 = (z-z2)/c2 = μ
x = a1λ+x1 , y = b1λ +y1 , z = c1λ + z1
x = a2μ +x2 , y = b2μ + y2 , z = c2μ + z2
STEP(2): If these two lines Intersect then it must be a common point.
a1λ+x1 = a2μ +x2 , b1λ +y1 = b2μ + y2
c1λ + z1 = c2μ + z2
STEP(3): solve any two equation to find the value of λ and μ , after finding the value of λ and μ put its value into the coordinates of the general points in step 1.
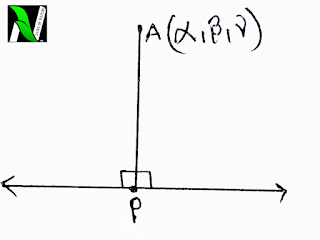
PERPENDICULAR FROM A POINT TO A LINE
Let any equation of a line is
(x-x1)/l =(y-y1)/m = (z-z1)/n = r say
and A(α,β,γ) is the given points , then
1). The coordinates of the foot of the perpendicular from the point A to the line is –
P(lr+a , mr+b , nr+c)
2). The length of the perpendicular AP is ;
√(lr+a-α)^2 +(mr+b-β)^2 +(nr+c-γ)^2
3). The equation of the perpendicular is given by
VECTOR FORM
The length of the perpendicular from the A(r1) to a line r = a + λb is = |(a-r1)×b|/|b|
SKEW LINES
It is the two straight lines in the space which are not parallel and not intersecting. It means, two skew lines are never be coplanar.
SHORTEST DISTANCE
If l1 and l2 are two skew lines then the perpendicular line on that skew lines give the shortest distance.
There is one and only one perpendicular line between two skew lines, which give the shortest distance.
CALCULATION OF SHORTEST DISTANCE
VECTOR FORM
If the vector equation of two skew lines are
r = a1+λb1 and r = a2+μb2 , then the shortest distance is –
d = |(a2-a1).(b1×b2)|/|b1×b2|
CARTESIAN FORM
If the two skew lines are
(x-x1)/l1 = (y-y1)/m1 = (z-z1)/n1 and
(x-x2)/l2 = (y-y2)/m2 = (z-z2)/n2 , then the shortest distance is given as –
POINTS TO BE REMEMBERED |
| 1). Shortest distance between the two parallel lines r = a1+λb and r = a2+μb is given by – d = |(a2-a1)×b2|/|b|2). If the two lines r = a1+λb1 and r = a2+μb2 get Intersect , means d = 0 , then (a2-a1).(b1×b2) = 0 |
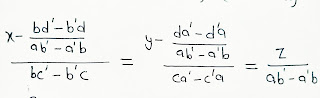
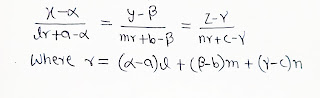
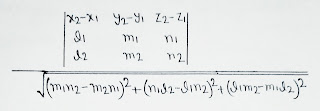
Well researchedwork!!